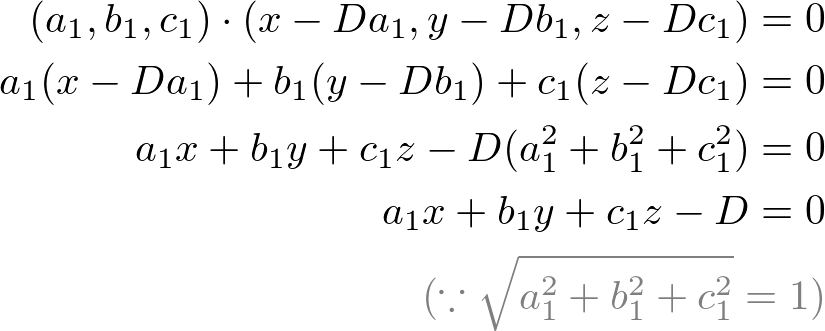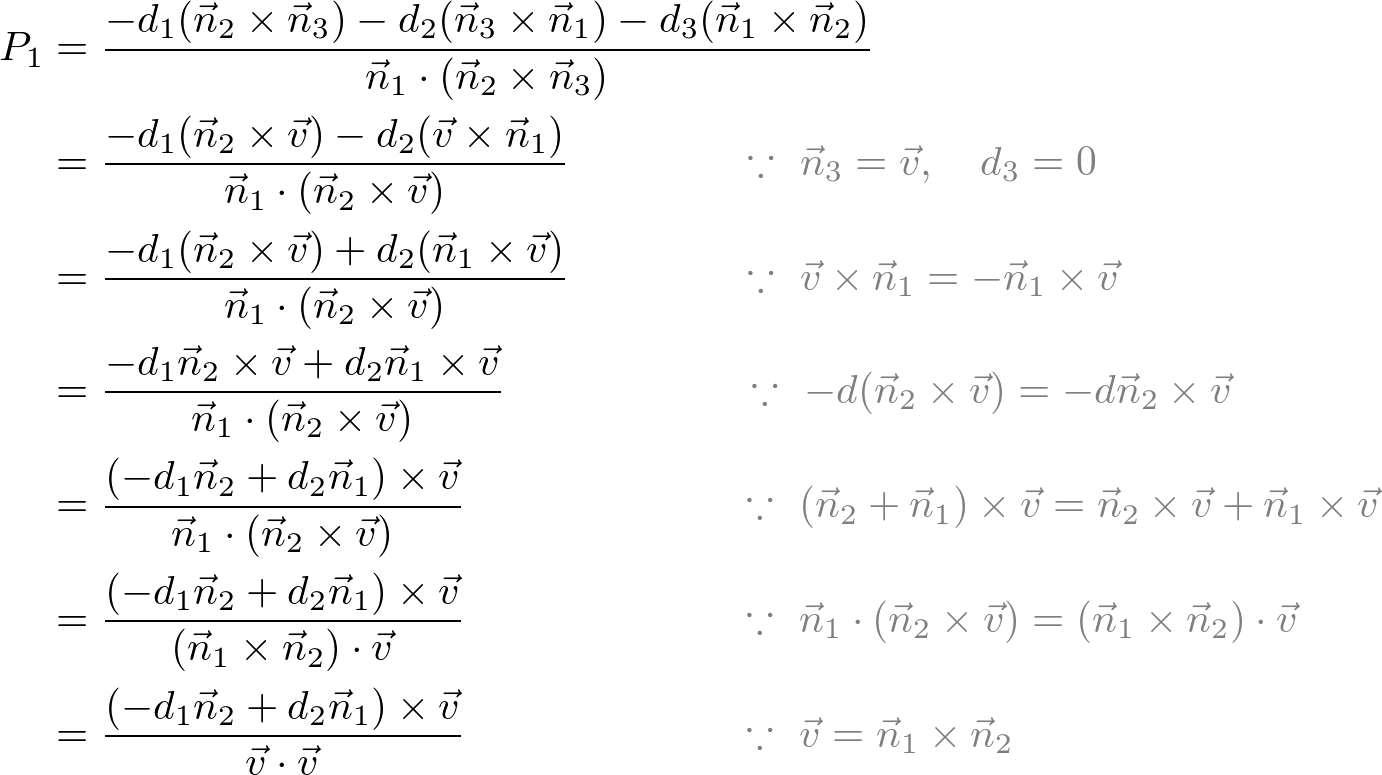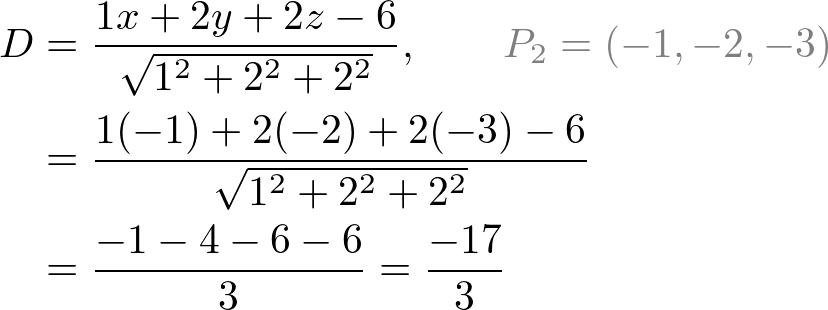Perpendicular Vector To Plane 3d

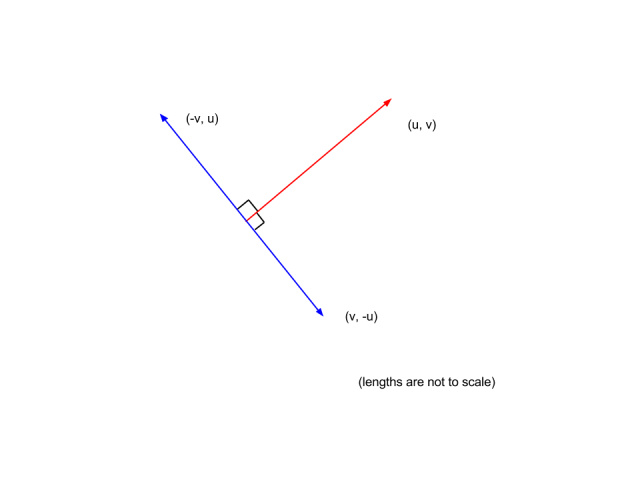
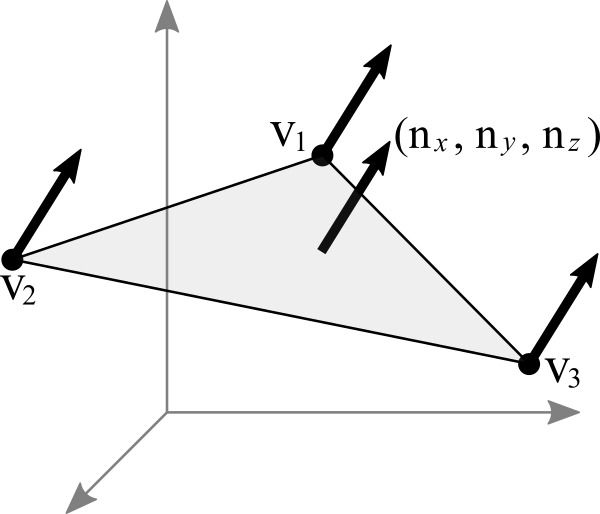
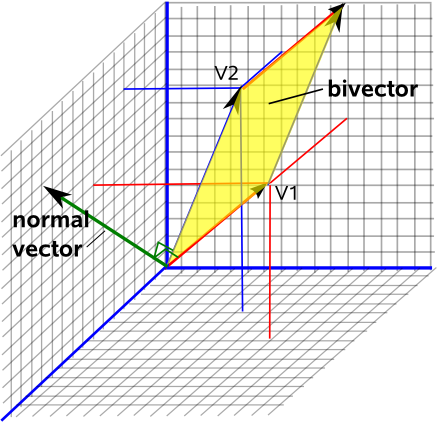
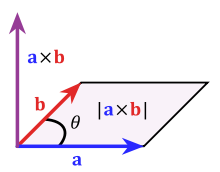
As the cross product of two vectors produces a vector perpendicular to both we will use the cross product of v1 and v2 to find a vector u perpendicular to the plane containing them.
Perpendicular vector to plane 3d. Sorry for the newbie question. These are the only two directions in the two dimensional plane perpendicular to the given vector. A 2 5 1 b 1 1 3 these vectors generate a plane. The word normal is also used as an adjective.
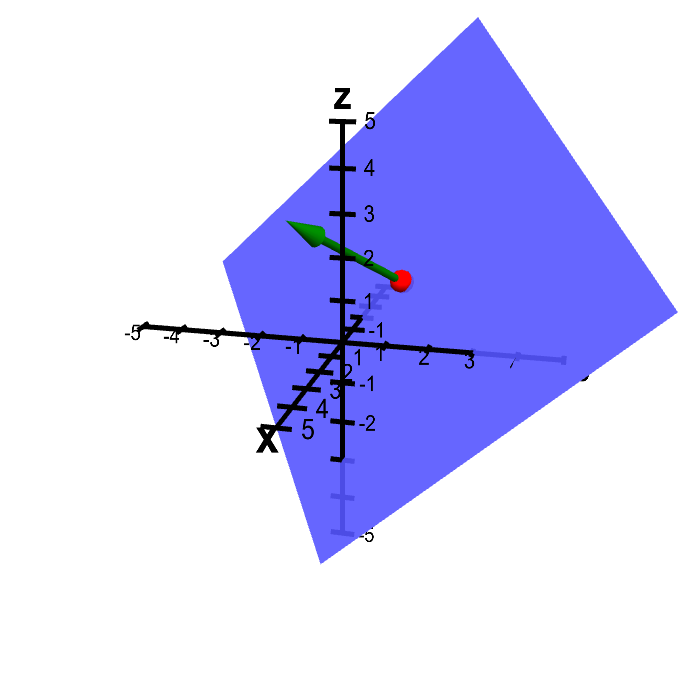
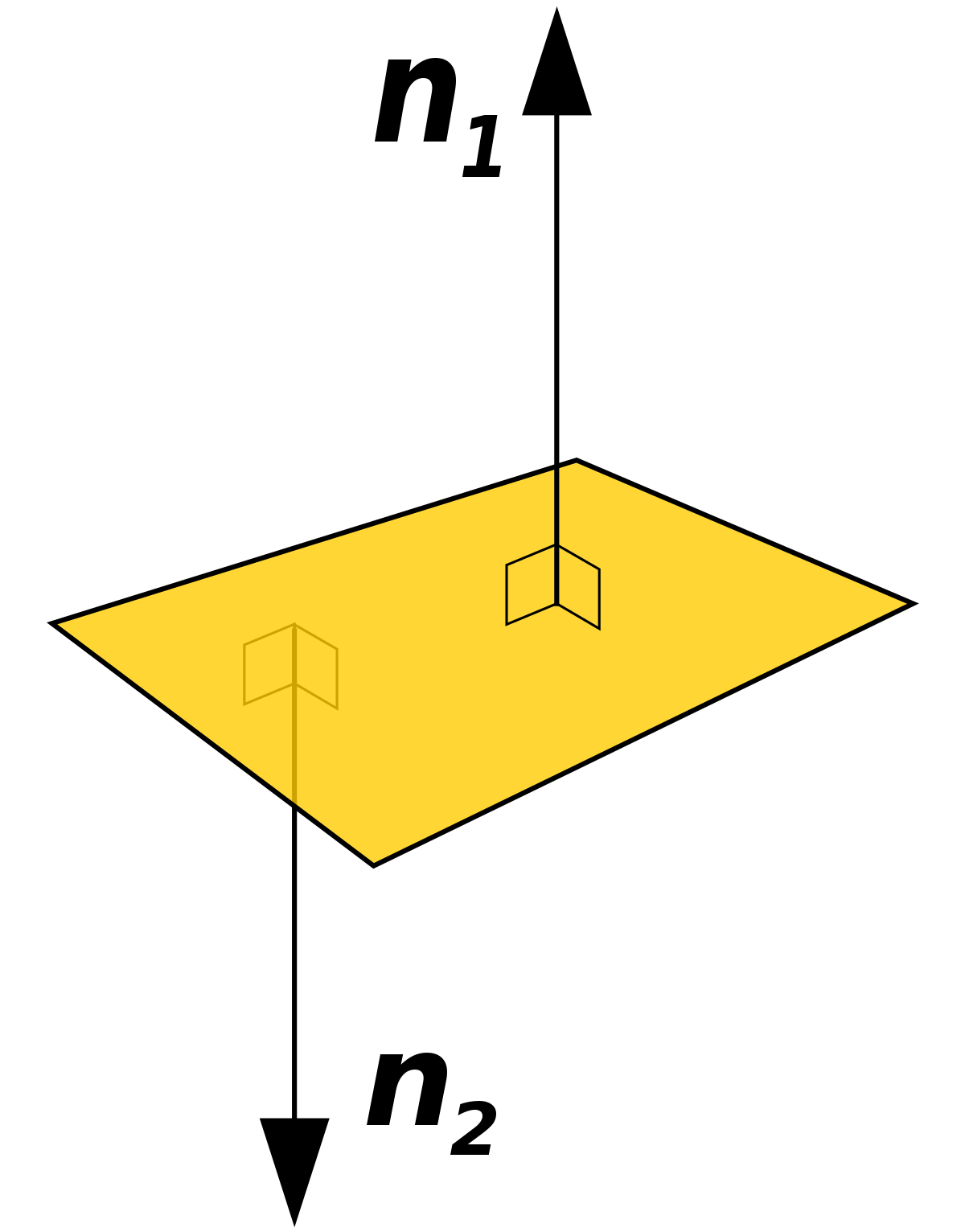
So what the equation tells us is that is perpendicular to all directions in the plane. For example in case the vector is 0 0 1 this is the generator of the z axis. That is is normal to the plane. In three dimensions a surface normal or simply normal to a surface at point p is a vector perpendicular to the tangent plane of the surface at p.
The vector v 1 0 3 is perpendicular to u 3 10. If a vector is perpendicular to two vectors in a plane it must be perpendicular to the plane itself. But any direction vector in the plane can be written in the form since is a fixed point in the plane and is the coordinates position vector of any given point. Step 2 find a vector perpendicular to the plane.
Which is the same as the normal vector of the plane. If you chose v1 1 you would get the vector v 1 0 3 which points in the opposite direction of the first solution. Calculate 3d vector perpendicular to a plane generated by two vectors. There are infinite solutions of vectors in 3d perpendicular to a given one in fact those solutions form a plane in the vector space sense that is a 2 dimensional vector space of solutions if you know what that means.
Square end aligned 3 x 2 3 y 1 0 z 3 x y 1. A plane in 3d coordinate space is determined by a point and a vector that is perpendicular to the plane. I am new to dealing with 3d and even simple stuff makes my head spin around. You can scale the new vector to whatever magnitude you want.
Active 10 years 10 months ago. This plane is to be defined by a position and normalised direction in addition to lying along p0 and p1 and facing p2 the plane should also be perpendicular to the plane created by p0 p1 and p2 i ve struggled with this for quite a while and any help anyone can offer is greatly appreciated. How can i get a third vector. Thus the equation of the plane which passes through point a 2 1 3 a 2 1 3 is begin aligned 3 x 2 3 y 1 0 z 3 0 rightarrow x y 1 0.
Lets say i have 2 vectors. Ask question asked 10 years 11 months ago.