Parallel Vectors Dot Product 3d

How to tell if two 3d vectors are in the same direction.

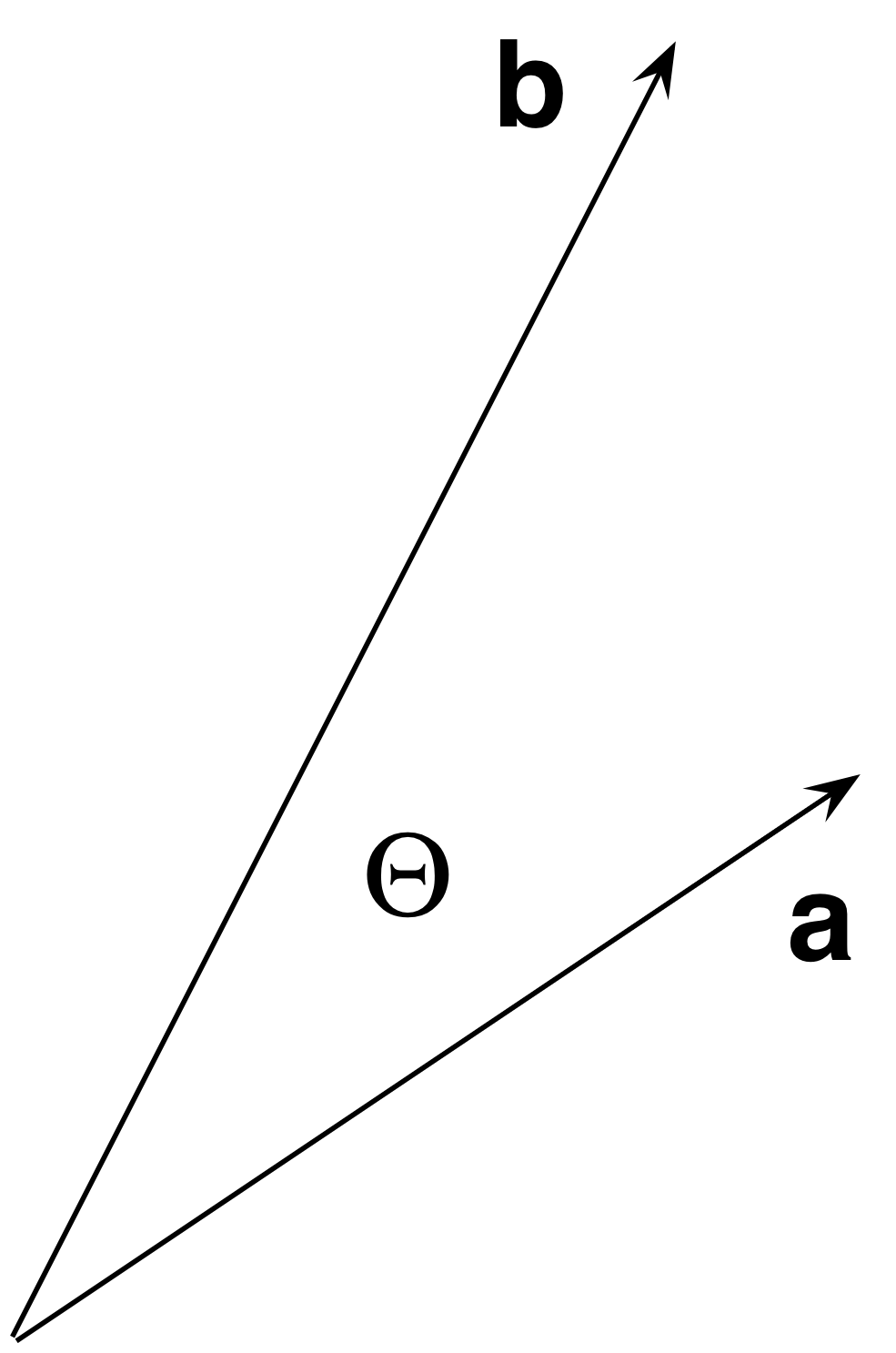
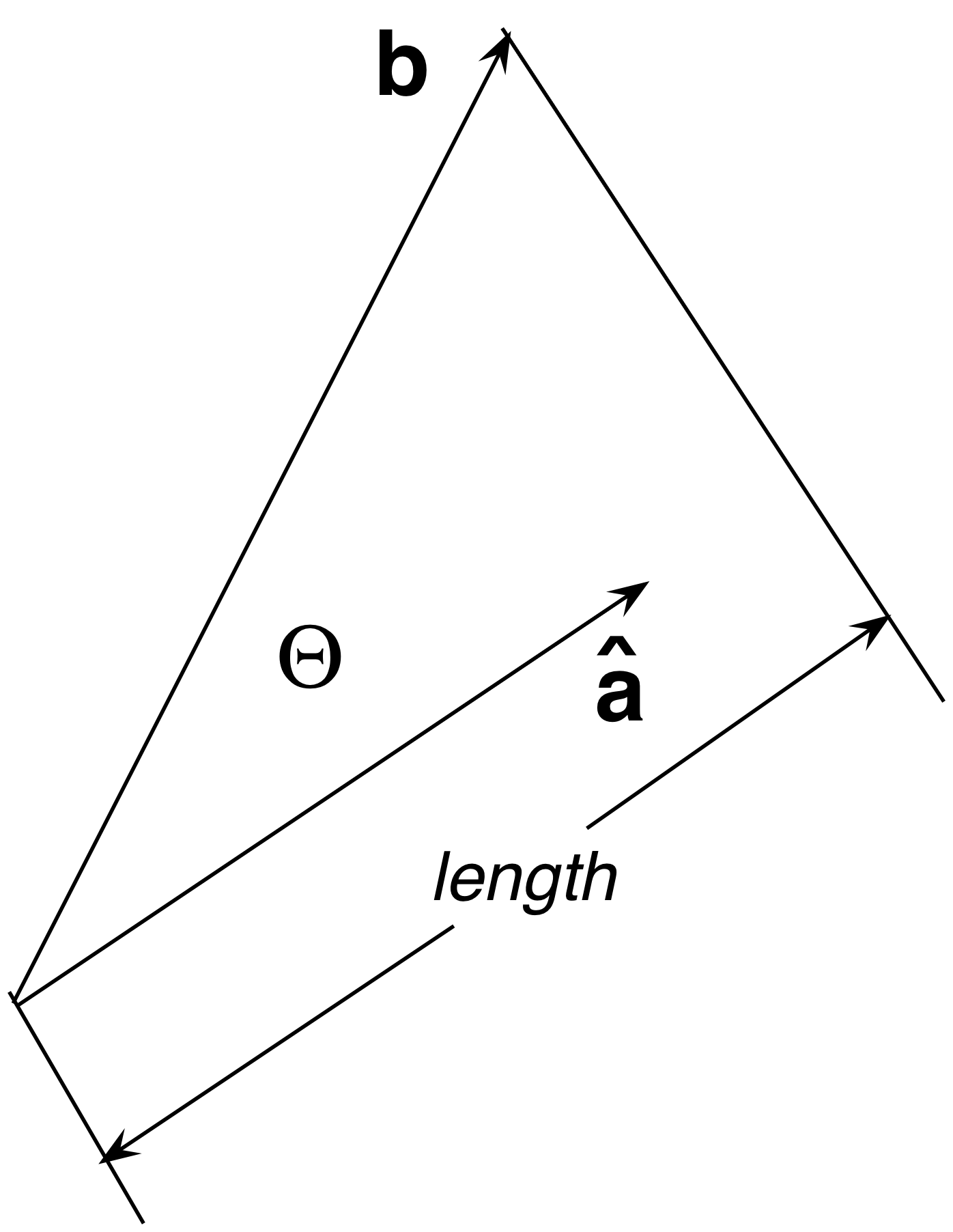
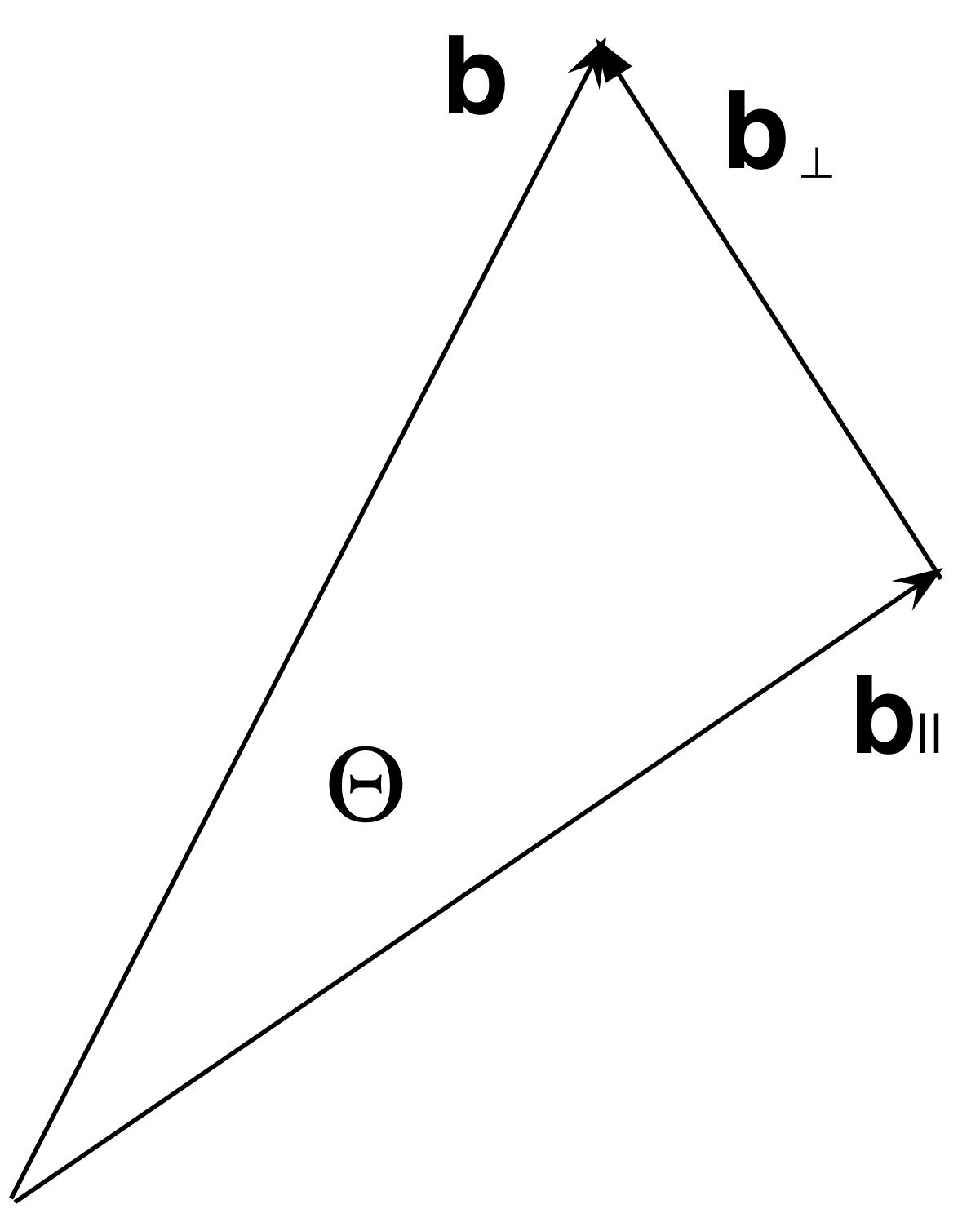
Parallel vectors dot product 3d. Scalar or dot product of two vectors the scalar or dot product of two vectors vec u and vec v is a scalar quantity defined by. A plane in r3 is determined by a point a b c on the plane and two direction vectors v and u that are parallel to the plane. Two vectors are parallel if they are scalar multiples of one another. The dot product of two parallel vectors is equal to the algebraic multiplication of the magnitudes of both vectors.

How to determine if the given 3 dimensional vectors are parallel. Then the dot product is. Ask question asked 6 years. Let a a 1 a 2 a 3 t.

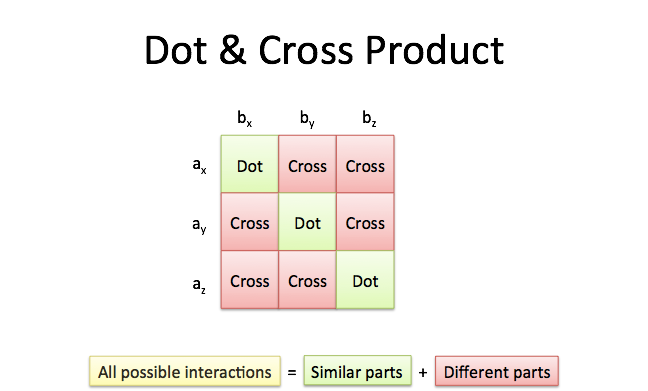
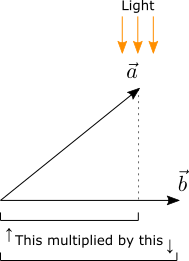
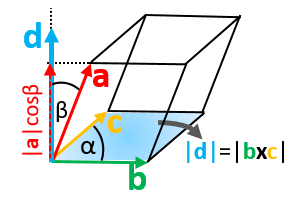
You may already be familiar with the dot product also called scalar product. The scalar or dot product and cross product of 3 d vectors are defined and their properties discussed and used to solve 3d problems. Vectors are parallel if the cross product is zero. The dot product also called scalar product of two vectors is one of the two ways we learn how to multiply two vectors together the other way being the cross product also called vector product.

The dot product is defined for 3d column matrices. They have same oriented direction if their cross product is zero and dot product is greater. Recall how to find the dot product of two vectors and recall that for a vector. If the two vectors are in the same direction then the dot product is positive.

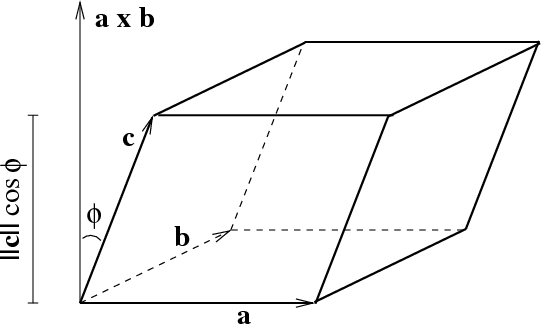
In this example the cross product yields 3 0 2 hence they are not parallel i e in the same direction. Geometrically the cross product of two vectors is the area of the parallelogram between two vectors are perpendicular if their dot product is zero and parallel if their dot product is 1. If u and v are two non zero vectors and u cv then u and v are parallel. Multiply corresponding elements of both column matrices then add up all the products.

The idea is the same. Determine which vectors are. Given two vectors vec u and vec v we refer to the scalar product by writing. How to define parallel vectors.

Let b b 1 b 2 b 3 t. If they are in the opposite direction then the dot product is negative. Cross product in 3d in this explainer we will learn how to find the cross product of two vectors in space and how to use it to find the areas of geometric shapes. There are two ways to multiply vectors together.

The following diagram shows several vectors that are parallel.